Примечание. Текст задачи взят с форума

Задача.
Диагональным сечением правильной четырехугольной призмы является квадрат, площадь которого равен 144 квадратных сантиметров.
Найдите объем объем призмы.

Решение.
Поскольку, согласно определению диагонального сечения призмы, оно проходит через диагональ основания, а данная призма является правильной и четырехугольной, то данное диагональное сечение проходит через диагональ основания, которое является квадратом.

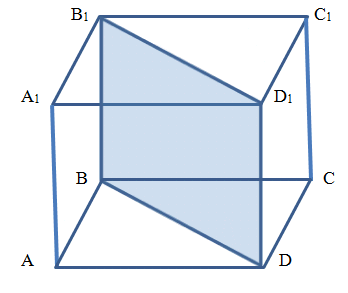
Исходя из того, что площадь диагонального сечения является квадратом (BB1DD1), то сторона квадрата (она же равна высоте призмы) равна:

а = √144 = 12 см

Как мы уже показали, в основании данной призмы также лежит квадрат ABCD, диагональ которого мы только что определили.

Таким образом, если обозначить сторону квадрата как b, получим:

b² + b² = 12²
или
2b² = 144
b² = 72

Заметим, что площадь основания (квадрата ABCD) равна  
S = b²
то есть
S = 72

Согласно формуле нахождения объема призмы
V = Sh

Подставим значения:
V = 72h
высота сечения равна высоте прямой призмы и это значение было найдено нами ранее, то есть
V = 72 * 12 = 864 см³

Ответ: 864 кубических сантиметра