Задача.  
  ABCD - квадрат с стороной 4 см.Точка М отдалена от каждой вершины квадрата на 7 см. Найти расстояние от середины отрезка МА до вершин и сторон квадрата.  

Решение.
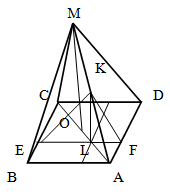
Сначала изобразим условие задачи графически.

Как видно из чертежа, точка М - представляет собой вершину правильной четырехугольной пирамиды. Точка К, явлющаяся серединой ребра АМ, Является точкой, к которой проведены медианы треугольников ADM, ABM и ACM. То есть медианы KC, KD и KB этих треугольников и являются расстояниями до вершин квадрата.

Таким образом, задача нахождения расстояний сводится к задаче нахождения длины этих медиан.

Для нахождения длины медиан применим теорему Стюарта.

m_c² = ( 2a² + 2b² - c² ) / 4

Для треугольника ABM медиана KB
KB² = ( 2AM²   + 2AB² - AM²  )  / 4
KB² = ( 2 * 7 ² + 2 * 4 ² - 7 ² ) / 4
KB² = ( 98 + 32 - 49  ) / 4 = 81 / 4
KB = 4,5 

Поскольку пирамида правильная, то для KD будет тот же результат KD = 4,5

Длина диагонали квадрата АС = 4√2 (по соответствующей формуле d = a√2 )

Для треугольника ACM медиана CK будет равна:
CK² = ( 2AC² + 2CM² - AM²  )  / 4
CK² = ( 2(4√2)² + 2 * 7² - 7²  )  / 4
CK² = ( 64 + 98 - 49  )  / 4
CK = √113/2

Для нахождения расстояний до сторон квадрата изобразим задачу следующим образом:

Сначала определим высоту пирамиды:  
MO²  = MA² -  OA²

Поскольку пирамида правильная, длина OA равна половине длины диагонали квадрата.
MO² = 7² - ( 2√2 )² 
MO = √41

Откуда длина отрезка KL по теореме Фалеса равна 
KL = √41/2
(так как KA равно половине MA в треугольнике AOM или, если хотите, как средняя линия треугольника)

Аналогично,
LA = OA / 2 = √2

LA является диагональю квадрата, стороны которого равны расстоянию от точки L до сторон основания. Поскольку диагональ квадрата равна 
d = a√2
то
LA = a√2
√2 = a√2  
  a = 1

То есть LF = 1

Тогда расстояние от точки K до стороны AD по теореме Пифагора будет равно:
KF² = KL² + LF²
KF² = ( √41/2 )² + 1
KF = √45 / 2 = 3√5 / 2

Теперь найдем расстояние до двух других сторон квадрата
KE² = KL² + LE²

заметим, что LE = FE - LF = AB - LF = 4 - 1 = 3

Откуда
KE² = ( √41/2 )²  + 3²
KE = √77 / 2

Ответ: расстояния до вершин квадрата равны 4,5 4,5   √113/2, а до сторон  квадрата √77/2 и   3√5/2