Цилиндр и его сечения (квадрат и вписанный куб)

Примечание. Это урок с решениями задач по геометрии (раздел цилиндр). Если Вам необходимо решить задачу по геометрии,
которой здесь нет - пишите об этом в форуме. В задачах вместо символа "квадратный корень" может использоваться знак "√".

Задача

Осевое сечение цилиндра - квадрат, диагональ которого равна 4√2.
Вычислить объем цилиндра.
Цилиндр с сечением

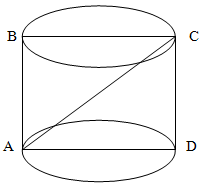
Решение.
Поскольку диагональ сечения цилиндра - квадрат, то обозначим его сторону как a.
a² + a² = (4√2)²
2a² = 32
a² = 16
a = 4

Объем цилиндра найдем по формуле:
V = πd² / 4 * h
откуда
V = π4² / 4 * 4
V = 16π

Ответ: Объем цилиндра равен 16π

Задача

Куб с ребром длиной а вписан в цилиндр. Найдите площадь осевого сечения цилиндра.

Решение.
Проведем плоскость через основание цилиндра.
Квадрат вписанный в круг

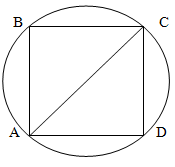
Диагональ куба является одновременно диаметром цилиндра. Зная сторону куба, определяем длину диагонали AC квадрата ABCD как
CD² + AD²= AC²
a² + a² = AC²
2a² = AC
AC = a√2

Проведем плоскость через ось цилиндра по диагонали AC. Высота сечения равна длине ребра куба и по условиям задачи рана а, а ширина сечения равна a√2.
Таким образом, площадь сечения равна:

S = a * a√2 = a²√2

Ответ: a²√2

Задача

Диагональ осевого сечения цилиндра равна 12 см и образует с плоскостью нижнего основания угол 45 градусов. Найти обьём цилиндра.

Решение.
Поскольку основание осевого сечения образует с высотой цилиндра, принадлежащей сечению, прямой угол, то треугольник, который образован диагональю осевого сечения, высотой цилиндра и его диаметром - прямоугольный.

Исходя из этого, угол между диагональю и высотой также равен 45 градусов ( 180 - 90 - 45 ).

Таким образом, треугольник является равнобедренным, а, следовательно, высота цилиндра равна его диаметру. Применив теорему Пифагора, найдем их.

d² + d² = 12²

2d² = 144
d² = 72

Теперь применим формулу объема цилиндра V = пd² / 4 h

V = 72п / 4 * √72
V = 18п * √72 = 108п * √2

Ответ: 108п * √2

Задача

Высота цилиндра 2м. Радиус основания 7м. В этот цилиндр наклонно вписан квадрат так, что все вершины его лежат на окружностях оснований. Найти сторону квадрата.

Решение.

В силу симметричности квадрата и цилиндра и ввиду того, что квадрат наклонный, диагональ квадрата пересечет ось цилиндра ОО₁ в точке М, являющейся серединой отрезкаОО₁. По условию ОО₁=2м, а ОА=7 м, поэтому ОМ=1м.

Пусть d – диагональ квадрата. Тогда сторона квадрата а равна:

Решение задачи про сечение цилиндра и нахождение его диагонали. Рішення задачі про перетин циліндра і знаходження його діагоналі.

Цилиндр и его сечения | Описание курса | Осевое сечение цилиндра