Примечание. Текст задачи взят с форума.

Задача.
В равнобедренной трапеции АBCD проведена диагональ АС равная 15 см и задан угол САD.
Найти высоту трапеции.

Решение.

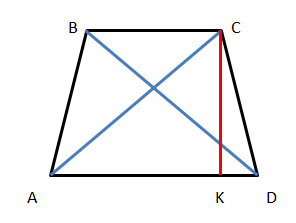
Диагональ AC, сторона CD и основание трапеции AD образуют треугольник. Опустим из его вершины высоту CK, которая, одновременно, будет являться и высотой заданной трапеции.

Поскольку CK - высота, то треугольник ACK, образованный данной высотой - прямоугольный.  При этом угол ∠CAK = ∠CAD, так как точки K и D лежат на одной прямой.
Таким образом:

sin ∠CAK = CK / AC
(это следует из самого определения синуса - противолежащий катет мы делим на гипотенузу)

откуда легко найти высоту заданной трапеции:

CK = AC * sin  ∠CAK
или
CK = 15 sin ∠CAD

Примечание. Если угол CAD был бы задан, можно было бы воспользоваться таблицей значений тригонометрических функций.