|
|
Задача.
Основание прямой призмы - ромб с углом 120 градусов. БОльшая диагональ призмы равна 8см и составляет с боковым ребром угол 60 градусов. Найти сторону ромба и меньшую диагональ призмы.
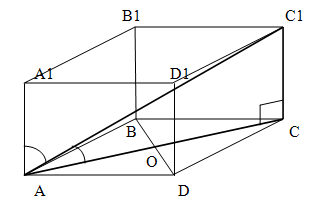
Решение.
Поскольку диагональ AC1 образует с ребром AA1 угол 60 градусов, призма является прямой, то угол C1AC равен 90 - 60 = 30 градусов.
Исходя из этого cos 30 = AC / AC1 = √3 / 2
AC / AC1 = √3 / 2
AC / 8 = √3 / 2
2AC = 8√3
AC = 4√3
Поскольку угол ADC равен 120 градусам, то угол BAD равен 60 градусам. (Сумма углов выпуклого четырехугольника равна 180(n-2) = 360 градусам, углы ромба попарно равны).
Исходя из того, что угол BAD равен 60 градусам, треугольники ABD и BDC- равносторонние. (Так как ABCD - ромб, то они равнобедренные, следовательно углы при основании равны, значит они равны ( 180 - 60 ) / 2 = 60 градусов. Треугольник, у которого все углы равны - равносторонний).
Диагонали параллелограмма в точке пересечения делятся пополам. Таким образом, AO = AC / 2 = 4√3 / 2 = 2√3
Поскольку треугольник ABD правильный, то AO является одновременно высотой и биссектрисой. Учтем, что высота правильного треугольника равна
h = а √3 / 2, тогда
а √3 / 2 = 2√3
а = 4
Зная, что BD = 4 см, DD1 = 4 см, по теореме Пифагора найдем меньшую диагональ:
BD12 = 4 + 4
Таким образом, сторона ромба равна 4 см, а, так как треугольники ABD и BDC- равносторонние, то и меньшая диагональ ромба равна 4 см.
Для того, чтобы найти длину ребра призмы, учтем, что диагональ AC1 = 8 см, а угол C1AC = 30 градусам. Тогда sin 30 = C1C / AC1 = 1/2
C1C / 8 = 1/2
C1C = 4 см
Зная что BD = 4 см (меньшая диагональ ромба), D1D = 4 см (ребро призмы), длину меньшей диагонали призмы найдем по теореме Пифагора:
BD12 = DD12 + BD2
BD12 = 42 + 42
BD12 = 32
BD1 = 4√2
Ответ: Сторона ромба - 4 см, меньшая диагональ призмы с ромбом в основании равна 4√2 см.
Параллелограмм в основании призмы |
Описание курса
| Пирамида. Решение задач
|

