|
|
Примечание. Это часть урока с задачами по геометрии (раздел параллелограмм). Если Вам необходимо решить задачу по геометрии, которой здесь нет - пишите об этом в форуме. Для обозначения действия извлечения квадратного корня в решениях задач используется символ √ или sqrt(), при чем в скобках указано подкоренное выражение.
См. также: Формулы, теоретический материал можно посмотреть по ссылке "Свойства и площадь параллелограмма".
Теоретический материал
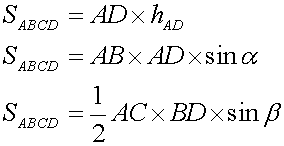
Пояснения к формулам нахождения площади параллелограмма:
- Площадь параллелограмма равна произведению длины одной из его сторон на высоту, опущенную на эту сторону
- Площадь параллелограмма равна произведению двух его смежных сторон на синус угла между ними
- Площадь параллелограмма равна половине произведения его диагоналей на синус угла между ними
Задачи на нахождение площади параллелограмма
Задача.
В параллелограмме меньшая высота и меньшая сторона равны 9 см и корню из 82 соответственно.Большая диагональ 15 см .Найти площадь параллелограмма.
Решение.
Обозначим меньшую высоту параллелограмма ABCD, опущенную из точки B на большее основание AD как BK.
Найдем значение катета прямоугольного треугольника ABK, образованного меньшей высотой, меньшей стороной и частью большего основания. По теореме Пифагора:
AB2 = BK2 + AK2
82 = 92 + AK2
AK2 = 82 - 81
AK = 1
Продлим верхнее основание параллелограмма BC и опустим на него высоту AN из его нижнего основания. AN = BK как стороны прямоугольника ANBK. У получившегося прямоугольного треугольника ANC найдем катет NC.
AN2 + NC2 = AC2
92 + NC2 = 152
NC2 = 225 - 81
NC2 = √144
NC = 12
Теперь найдем большее основание BC параллелограмма ABCD.
BC = NC - NB
Учтем, что NB = AK как стороны прямоугольника, тогда
BC = 12 - 1 = 11
Площадь параллелограмма равна произведению основания на высоту к этому основанию.
S = ah
S = BC * BK
S = 11 * 9 = 99
Ответ: 99 см2 .
Задача
В параллелограмме АВСД на диагональ АС опущен перпендикуляр ВО. Найдите площадь параллелограмма, если АО=8, ОС=6 и ВО=4.
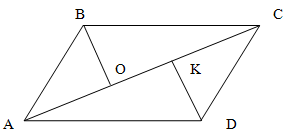
Решение.
Опустим на диагональ АС дополнительно еще один перпендикуляр DK.
Соответственно, треугольники AOB иDKC, COB и AKD попарно равны. Одна из сторон является противолежащей стороной параллелограмма, один из углов - прямой, так как является перпендикуляром к диагонали, а один из оставшихся углов является внутренним накрест лежащим для параллельных сторон параллелограмма и секущей диагонали.
Таким образом, площадь параллелограмма равна площади указанных треугольников. То есть
Sпаралл = 2SAOB +2SBOC
Площадь прямоугольного треугольника равна половине произведения катетов. Откуда
S = 2 ( 1/2 8 * 4 ) + 2 ( 1/2 6 * 4 ) = 56 см2
Ответ: 56 см2 .
Параллелограмм (часть 2) |
Описание курса
| Высота параллелограмма
|

