БИССЕКТРИСА УГЛА
Слово «биссектриса» с французского переводится как «надвое рассекающая». Биссектриса угла – это «равноделящая» угол, т.е. делящая угол пополам.
Биссектриса угла – луч, проведенный из вершины угла между его сторонами и делящий угол пополам.
Биссектрису угла можно построить по градусной мере угла с помощью транспортира. Для этого градусную меру заданного угла делят пополам и на одной из сторон от вершины откладывают градусную меру половинного угла. Вторая сторона такого угла будет биссектрисой заданного угла.
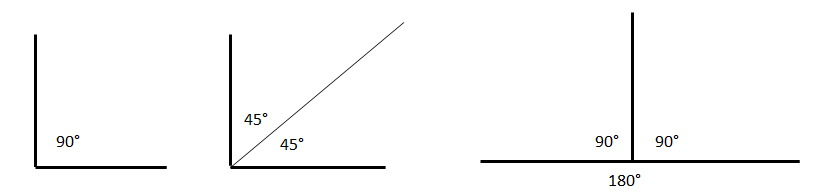
Если заданный угол имеет градусную меру 60°, то два построенных с помощью биссектрисы угла – по 30°, так как 60°:2=30°.
Развернутый угол разбивается биссектрисой на два прямых угла (180°:2=90°), любой тупой угол разбивается биссектрисой на два острых угла.
Построение биссектрисы угла с помощью циркуля и линейки
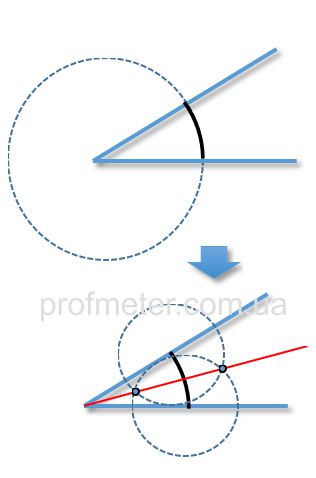
Чтобы построить биссектрису угла без транспортира, используя только циркуль и линейку, нужно выполнить следующие действия (см. рисунок выше).
- Из вершины угла, любым радиусом, необходимо провести дугу окружности, чтобы она пересекла стороны угла
- Из каждой точки (их две) пересечения дуги и стороны угла, снова провести души окружности (другим радиусом)
- Через любую из точек пересечения дуг дополнительно построенных окружностей, провести луч из вершины угла, который и будет биссектрисой этого угла
Биссектриса углов треугольника
Биссектрисой угла треугольника называется отрезок биссектрисы угла, проведенный от вершины угла до её пересечения с противолежащей стороной.
У треугольника существуют три биссектрисы, проведенные из каждой его вершины.
У биссектрисы угла треугольника существует масса особенных свойств, которые описаны в отдельной статье "Биссектриса углов треугольника".
В любом треугольнике ABC, кроме внутренней или просто биссектри́сы, можно провести и внешние биссектрисы, то есть биссектрисы углов, смежных с внутренними углами треугольника. При этом внутренняя и внешняя биссектриса одного и того же угла перпендикулярны. Подробнее об этом см. в статье "Биссектриса внешнего угла треугольника"
Вертикальные и смежные углы |
Описание курса
| Биссектриса углов треугольника
|

