Примечание. См. также формулы площади треугольника.

Задача

Площадь прямоугольного треугольника равна S, а один из острых углов равен α. Найти высоту, опущенную на гипотенузу.

Решение.

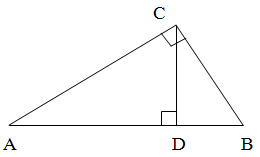
Площадь треугольника (S) будет равна:
S = 1/2 CD * AB

Пусть угол А равен α. Тогда
AC = AB cos α
(По определению косинуса   cos α = AC /AB)

Рассмотрим треугольник ADC. Поскольку CD - высота, опущенная на гипотенузу, то угол CDA - прямой. Таким образом
  CD = AC sin α

поскольку   AC = AB cos α, то  
CD = AB cos α sin α
откуда
AB = CD / ( cos α sin α )

Вернемся к изначальной формуле площади прямоугольного треугольника и подставим в нее найденные значения.
S = 1/2 CD * AB
S = 1/2 CD *  CD / ( cos α sin α )
S = 1/2 CD² / ( cos α sin α )

Поскольку все значения, кроме высоты CD треугольника нам известны, выразим высоту из формулы площади прямоугольного треугольника.
CD²  = 2S  cos α sin α
или
CD = √ ( 2S  cos α sin α )