Список предметов
Параллелограмм
84 / 191

Параллелограмм  - четырёхугольник, у которого противолежащие стороны попарно параллельны, то есть лежат на параллельных прямых.

Частными случаями параллелограмма являются прямоугольник, квадрат и ромб.

Как выглядит параллелограмм

Параллелограмм с проведенной высотой к одному из оснований и диагоналями  

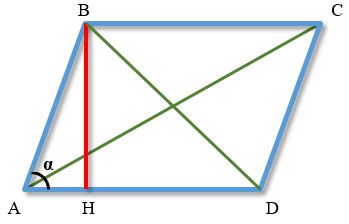
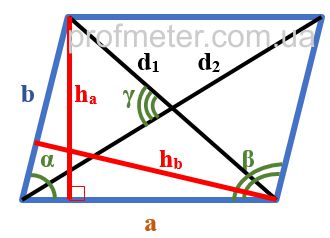
На приведенном рисунке параллелограмм обозначен синими линиями.

Элементы параллелограмма, указанные на рисунке:
ABCD - параллелограмм, у которого противолежащие стороны попарно параллельны ( AB параллельна CD, а BC параллельна AD)
BH - высота параллелограмма, опущенная из точки B на основание AD (на рисунке обозначена красным цветом)
AC и BD - диагонали параллелограмма.

Свойства параллелограмма

  • Противоположные стороны параллелограмма равны
  • Противоположные углы параллелограмма равны
  • Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам. Точка пересечения диагоналей называется центром симметрии параллелограмма
  • Диагональ делит параллелограмм на два равных треугольника
  • Сумма углов, прилежащих к одной стороне, равна 180°. (см. формулу ниже)
  • Сумма всех углов равна 360°
  • Средние линии параллелограмма пересекаются в точке пересечения его диагоналей и делятся этой точкой пополам
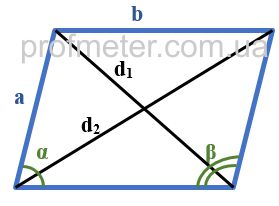
  • Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его сторон (см. формулу ниже)
Параллелограмм, с обозначенными длинами сторон a и b, а также углами альфа и бета, а также диагоналями d1 и d2
Основные тождества параллелограмма. Сумма квадратов диагоналей равна удвоенной сумме квадратов смежных сторон. Сумма углов, прилежащих к одной стороне равна 180 градусам

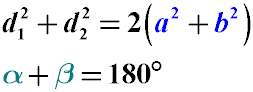
Признаки параллелограмма

Четырёхугольник ABCD является параллелограммом, если выполняется одно из следующих условий:
  • Противоположные стороны попарно равны
  • Противоположные стороны попарно параллельны и равны
  • Противоположные углы попарно равны
  • Диагонали делятся в точке их пересечения пополам
  • Сумма соседних углов равна 180 градусов
  • Две стороны равны и параллельны

Как найти площадь параллелограмма

Параллелограмм, с отмеченными на чертеже основаниями a и b, диагоналями d1 и d2, а также высотой h, проведенной к основанию a
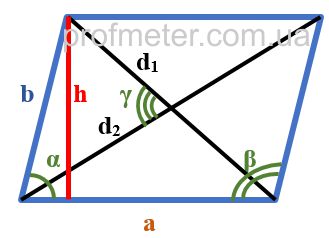
Формулы нахождения площади параллелограмма приведены ниже:

 Формулы нахождения площади параллелограмма через стороны, углы, высоту и диагонали и углы между ними
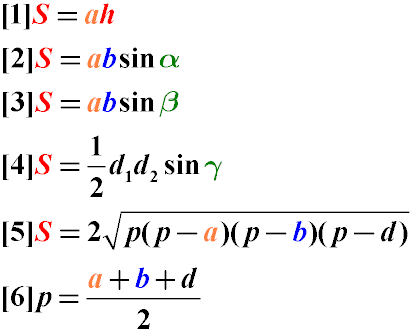
То есть:
  1. Площадь параллелограмма равна произведению длины одной из его сторон на высоту, опущенную на эту сторону
  2. Площадь параллелограмма равна произведению двух его смежных сторон на синус угла между ними. Как видно из чертежа, произведение b sin α равно высоте, опущенной на другую сторону, что в итоге дает нам предыдущую формулу
  3. Площадь параллелограмма равна произведению двух его смежных сторон на синус угла между ними
  4. Площадь параллелограмма равна половине произведения его диагоналей на синус угла между ними 
  5. Площадь параллелограмма также можно найти через формулу Герона, рассмотрев одну из диагоналей как треугольник и вычислив удвоенную площадь этого треугольника
  6. Для нахождения полупериметра треугольника из предыдущей формулы мы используем две стороны параллелограмма и его диагональ. Поскольку каждая диагональ разбивает его на два равных треугольника, то не имеет значения, какую из диагоналей мы выберем

Как найти стороны параллелограмма

Параллелограмм с отмеченными высотами h опущенными на соответствующую сторону, отмеченными углами между сторонами и углом между диагоналями, обозначенными диагоналями d1 и d2
Формулы для нахождения сторон параллелограмма через его диагонали и углы, а также через площадь и высоту
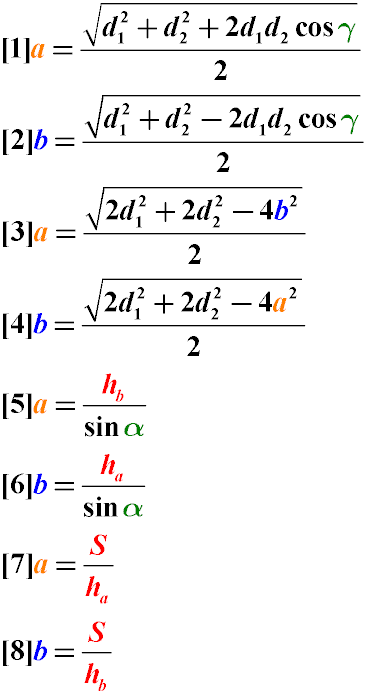
Стороны параллелограмма можно найти через:
  • Размеры диагоналей и угол между ними (формулы 1 и 2) 
  • Через длины диагоналей и одну из сторон можно найти вторую (формулы 3 и 4)
  • Через высоту, опущенную на сторону и угол между сторонами (формулы 5 и 6)
  • Через площадь и высоту, опущенную на заданную сторону, можно найти величину этой стороны (Формулы 7 и 8)

Как найти диагонали параллелограмма

Параллелограмм с отмеченными высотами h опущенными на соответствующую сторону, отмеченными углами между сторонами и углом между диагоналями, обозначенными диагоналями d1 и d2
Формулы нахождения диагоналей параллелограмма через известные значения длин его сторон, углов, площади или других сторон
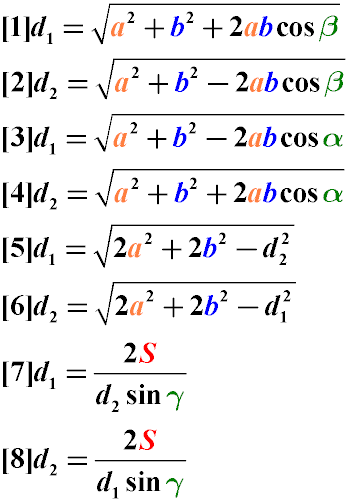
  • Диагональ параллелограмма можно найти через длины его сторон и косинус угла между ними (Формулы 1-4)
  • Также диагональ может быть найдена через длины сторон и размер второй диагонали (Формулы 5-6)
  • Диагональ может быть найдена из площади, длины второй диагоналями и угла между ними (Формулы 7-8)

Как найти периметр параллелограмма

Параллелограмм с отмеченными высотами h опущенными на соответствующую сторону, отмеченными углами между сторонами и углом между диагоналями, обозначенными диагоналями d1 и d2
Формулы для нахождения периметра параллелограмма через его стороны, высоты, опущенными на эти стороны и угол между сторонами
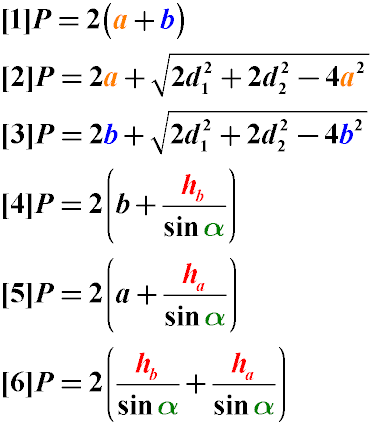
Периметр параллелограмма может быть найден:
  • через его стороны (Формула 1)
  • через одну из сторон и длину двух диагоналей (Формулы 2 и 3)
  • через сторону, высоту и угол между сторонами (Формулы 4-6)
Задачи с решениями про параллелограмм смотрите в уроках ниже:

Содержание главы:

0  


 Трапеция, описанная вокруг окружности | Описание курса | Параллелограмм. Задачи про площадь и стороны