Примечание. Текст задачи взят с форума.

Задача.
Из точки к плоскости прямоугольника со сторонами 9 см и 12 см, проведен перпендикуляр,основанием которого является одна из вершин прямоугольника.Расстояние от противоположной вершины прямоугольника до этой точки равно 39 см. Найдите расстояние от данной точки до плоскости прямоугольника.

Решение.

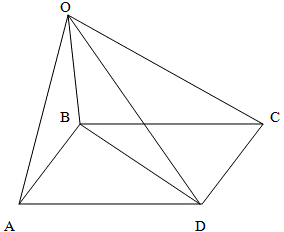
Пусть перпендикуляр к плоскости прямоугольника проведен из вершины В. Найдем длину диагонали прямоугольника BD.

BD является гипотенузой прямоугольного треугольника BCD, поэтому

BD² = BC² + CD²
BD²  = 9² + 12² 
BD²  = 225 
BD = 15

Точка О образует с противоположной вершиной прямоугольника также прямоугольный треугольник. Откуда высота перпендикуляра ОВ равна:

OD² = OB² + BD²
OB² = OD² - BD²
OB² = 1521 - 225
OB² = 1296
OB = 36

Ответ: Расстояние от точки до плоскости прямоугольника 36 см.