Задача. Нахождение площади боковой поверхности и высоты пирамиды

Площадь равнобедренного треугольника найдем по формуле (Формула 1 из списка): 

Подставив значения из условия задачи в Формулу 1, получим:
S = 5 √ ( (13 + 5) (13 - 5) )
S = 5 √ 144 = 60

Поскольку граней у пирамиды четыре, то площадь боковой поверхности будет равна сумме всех четырех граней:

60 * 4 = 240 см²

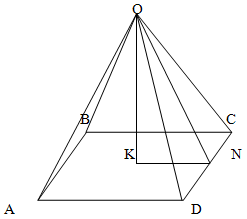
Так как по условию задачи, пирамида является правильной, то в основании ее лежит правильный многоугольник. Так как, согласно условию, она является четырехугольной, то данным многоугольником является квадрат.

Поскольку основанием пирамиды является квадрат, то: 

KN = 10/2 = 5 см

Поскольку каждая грань правильной пирамиды представляет собой равнобедренный треугольник, а в равнобедренном треугольнике медиана, биссектриса и высота, проведенные к третьей стороне совпадают, то
CN = 10/2 = 5 

Теперь найдем апофему пирамиды, исходя из свойств прямоугольного треугольника, образованного апофемой пирамиды, ребром и половиной основания (треугольником OCN).      

ON² + CN² = OC²
ON² + 25 = 169
ON² = 144
ON = 12 

Откуда уже несложно найти искомую высоту, исходя из свойств прямоугольного треугольника, образованного высотой пирамиды, ее апофемой и отрезком KN (треугольник ONK)              

OK²+ KN²= ON²
OK² + 25 = 144
OK = √119

Ответ: √119, 240 см² .