Свойства вписанной окружности
- В каждый треугольник можно вписать окружность, при этом только одну
- Центр вписанной окружности называется инцентром, он равноудалён от всех сторон
- Центр вписанной окружности является точкой пересечения биссектрис треугольника
Радиус вписанной окружности
Радиус вписанной в произвольный треугольник окружности равен отношению его площади к полупериметру.
Формулы радиуса вписанной окружности:
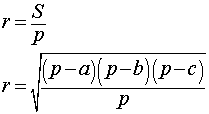
Центр вписанной в треугольник окружности - это точка пересечения биссектрис его улов. При этом стоит заметить, что для равнобедренного треугольника - биссектриса угла напротив основания - является одновременно и высотой.
Окружность, описанная вокруг треугольника (часть 2) |
Описание курса
| Четырехугольник
|

