|
|
Правильный Тетраэдр
Основные понятия и свойства
Тетраэдр - это правильный многогранник (правильная треугольная пирамида), у которого все грани являются правильными треугольниками.
Характеристики тетраэдра:
-
Все грани равны.
-
4 грани, 4 вершины и 6 рёбер.
-
Все двугранные углы при рёбрах и все трёхгранные углы при вершинах равны.
Элементы тетраэдра:
-
Медиана тетраэдра - это отрезок, соединяющий вершину с точкой пересечения медиан противоположной грани (медиан равностороннего
треугольника, противолежащего вершине).
-
Бимедиана тетраэдра - это отрезок, соединяющий середины скрещивающихся рёбер (соединяющий середины сторон треугольника,
являющегося одной из граней тетраэдра).
-
Высота тетраэдра - это отрезок, соединяющий вершину с точкой противоположной грани и перпендикулярный этой грани (то есть является
высотой, проведенной от любой грани, также совпадает с центром описанной окружности).
Свойства тетраэдра:
-
Все медианы и бимедианы тетраэдра пересекаются в одной точке.
-
Эта точка делит медианы в отношении 3:1, считая от вершины.
-
Эта точка делит бимедианы пополам.
Площадь, объем, высота, радиус вписанной и описанной сферы и другие формулы для тетраэдра

где:
a - длина ребра тетраэдра.
- Площадь поверхности S (Формула 1)
- Объем V (Формула 2)
- Высота правильного тетраэдра h (Формула 3)
- Радиус вписанной сферы r: Вписанная сфера касается всех граней тетраэдра в их центрах (Формула 4)
- Радиус описанной сферы R: Описанная сфера проходит через все вершины тетраэдра. (Формула 5)
Практические примеры
Примечание. Это часть урока с задачами по геометрии (раздел стереометрия, задачи о пирамиде).
Если Вам необходимо решить задачу по геометрии, которой здесь нет - пишите об этом в форуме.
В задачах вместо символа "квадратный корень" применяется знак "√".
Задача.
Найдите площадь поверхности треугольной пирамиды, у которой каждое ребро равно √3
Решение.
Поскольку все ребра треугольной пирамиды равны - она является правильной.
Площадь поверхности правильной треугольной пирамиды равна S = a2√3 .
Тогда
S = 3√3
Ответ: 3√3
Задача.
Все ребра правильной треугольной пирамиды равны 4 см. Найдите объем пирамиды
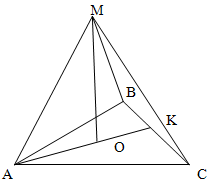
Решение.
Поскольку в правильной треугольной пирамиде высота пирамиды проецируется в центр основания,
который одновременно является центром описанной окружности, то
AO = R = √3 / 3 a
AO = 4√3 / 3
Таким образом, высота пирамиды OM может быть найдена из прямоугольного треугольника AOM
AO2 + OM2 = AM2
OM2 = AM2 - AO2
OM2 = 42 - ( 4√3 / 3 )2
OM2 = 16 - 16/3
OM = √(32/3)
OM = 4√2 / √3
Объем пирамиды найдем по формуле V = 1/3 Sh
При этом площадь основания найдем по формуле S = √3/4 a2
V = 1/3 (√3 / 4 * 16 ) ( 4√2 / √3 )
V = 16√2 / 3
Ответ: 16√2 / 3 см
Площадь боковой поверхности правильной треугольной пирамиды |
Описание курса
| Задачи про Тетраэдр
|

