Описание курса Аксиомы планиметрии Аксиома принадлежности точек и прямых Аксиома расположения точек на прямой Аксиома про длину отрезков Аксиома расположения точек относительно прямой Аксиома свойств измерения углов Аксиома свойств откладывания отрезков Аксиома свойств откладывания углов Существование треугольника, равного данному Свойство параллельных прямых Точки, отрезки и прямые Геометрическое место точек. Метод геометрических мест Отрезки в координатной плоскости Прямые на координатной плоскости Пересекающиеся прямые Луч Векторы Центральная и осевая симметрия Угол. Углы на плоскости Вертикальные и смежные углы Биссектриса угла Биссектриса углов треугольника Биссектриса внешнего угла Биссектриса. Примеры решения задач Площадь геометрической фигуры Окружность. Уравнение окружности Задачи про окружность Хорда Эллипс Треугольник Высота треугольника Сумма углов треугольника Площадь треугольника Медиана треугольника Как найти длину медианы треугольника Нахождение площади через медианы Угол между высотой и медианой треугольника Медиана прямоугольного треугольника Подобие треугольников Простейшие задачи на подобие треугольников Подобие треугольников. Первый признак подобия Подобие треугольников. Третий признак подобия Подобие треугольников. Использование в задачах Прямоугольный треугольник Прямоугольный треугольник Биссектриса в прямоугольном треугольнике Высота в прямоугольном треугольнике Высота в прямоугольном треугольнике (Часть 2) Теорема Пифагора и ее доказательство Применение теоремы Пифагора Гипотенуза прямоугольного треугольника Перпендикуляр к плоскости прямоугольного треугольника Равнобедренный треугольник Равнобедренный треугольник Рівнобедрений трикутник Площадь равнобедренного треугольника Площа рівнобедреного трикутника Углы равнобедренного треугольника Высота равнобедренного треугольника Окружность, вписанная в равнобедренный треугольник Окружность, описанная вокруг треугольника Окружность, описанная вокруг треугольника Окружность, описанная вокруг треугольника (часть 2) Вписанная в треугольник окружность Четырехугольник Существование четырехугольника с заданными сторонами Периметр четырехугольника Окружности, вписанные и описанные вокруг четырехугольника Углы четырехугольника Правильный четырехугольник (квадрат). Правильний чотирикутник (квадрат) Ромб Трапеция Площадь трапеции Высота трапеции Трапеция (задачи про основания) Диагонали трапеции Прямоугольная трапеция Равнобокая (равнобедренная) трапеция Углы равнобокой (равнобедренной) трапеции Высота равнобедренной трапеции Равнобокая трапеция Равнобокая трапеция (часть 2) Трапеция, описанная вокруг окружности Параллелограмм Параллелограмм. Задачи про площадь и стороны Параллелограмм (часть 2) Площадь параллелограмма Высота параллелограмма Прямоугольник Периметр прямоугольника Периметр и площадь прямоугольника Тригонометрия Синус Теорема синусов Задачи на решение с помощью теоремы синусов Теорема синусов (часть 2) Косинус Основное свойство функции косинуса Теорема косинусов и ее доказательство Теорема косинусов. Пример решения задачи Тангенс и его свойства Тригонометрические соотношения в прямоугольном треугольнике Тригонометрический круг Радианы и градусы. Радiани i градуси Таблица значений тригонометрических функций Синус, ко синус, тангенс угла 15 градусов (sin 15 cos 15 tg 15) Синус, косинус и тангенс угла 30 градусов (sin cos tg 30) - таблица значений Синус, косинус, тангенс угла 45 градусов (sin 45, cos 45, tg 45) Синус, косинус, тангенс угла 30 и 60 градусов (sin cos tg 30 и 60) Синус, косинус, тангенс угла 105 градусов (sin 105 cos 105 tg 105) Синус, ко синус, тангенс угла 120 градусов (sin 120 cos 120 tg 120) Тригонометрические тождества и преобразования Пояснение (доказательство) простейших тригонометрических тождеств Преобразования тригонометрических функций вида (α + a/bπ) и доказательство Тригонометрические формулы понижения степени sin cos tg Косинус двойного угла Многоугольники Правильный многоугольник Шестиугольник и его свойства Сумма углов многоугольника Стереометрия Прямые и плоскости Параллельность плоскостей. Свойства и признаки параллельности. Параллельные плоскости Перпендикулярные плоскости Прямые на плоскости Точка и плоскость Отрезок, пересекающий плоскость Наклонная из точки к плоскости Параллелограмм, рассеченный плоскостью Параллелограмм и плоскость Перпендикуляр к квадрату Перпендикуляр к плоскости прямоугольного треугольника Призма. Параллелепипед. Куб. Решение задач Объем призмы Площадь боковой поверхности призмы Прямая призма Правильная четырехугольная призма Куб Диагональное сечение правильной призмы Параллепипед Площадь поверхности и объем параллелепипеда Призма с треугольником в основании Призма с правильным треугольником в основании Призма с правильным треугольником в основании (часть 2) Призма с треугольником в основании ( часть 2) Призма с треугольником в основании ( часть 3) Параллелограмм в основании призмы Ромб в основании призмы Пирамида. Решение задач С треугольником в основании Пирамида с прямоугольным треугольником в основании Пирамида с равнобедренным треугольником в основании Правильная треугольная пирамида (правильная пирамида с треугольником в основании) Периметр основания правильной треугольной пирамиды Объем правильной треугольной пирамиды Площадь поверхности правильной треугольной пирамиды Площадь боковой поверхности правильной треугольной пирамиды Правильный тетраэдр Задачи про Тетраэдр Пирамида и вписанный конус Правильная пирамида Апофема правильной пирамиды Объем правильной усеченной пирамиды Правильная пирамида с четырехугольником в основании Задачи про правильную четырехугольную пирамиду Нахождение боковой поверхности и высоты правильной пирамиды с четырехугольником в основании Правильная пирамида с четырехугольником в основании (часть 3) Нахождение углов пирамиды Нахождение величины наклона боковых граней правильной прамиды Нахождение расстояний в правильной четырехугольной пирамиде С четырехугольником в основании Пирамида Неправильная пирамида с прямоугольником в основании Неправильная пирамида с четырехугольником в основании Сфера. Шар. Куля Сфера (Шар) Площадь сферы Полусфера Соотношение объема шара и конуса Цилиндр Задачи про цилиндр со вписанной призмой Цилиндр и его сечения Цилиндр и его сечения (квадрат и вписанный куб) Осевое сечение цилиндра Площадь поверхности цилиндра Конус Конус Площадь боковой поверхности конуса Объем конуса Объем конуса (2)

Задача На диагонали МР прямоугольника МNРQ отложены равные отрезки МА и РВ. Докажите, что АNBQ параллелограмм. Решение. Четырехугольник является параллелограммом, если его противоположные стороны попарно равны. Докажем это. Исходя из условия задачи треугольники MAN и PBQ равны. Так как PB = AM по условию задачи, PQ = NM как противоположные стороны прямоугольника, а углы BPQ и NMA равны, как внутренние накрест лежащие для параллельных прямых NP и MQ и секущей MP. Аналогично доказывается равенство треугольников NBP и QAM. Поскольку описанные треугольники равны, то NA = BQ,  NB = BQ. Таким образом, поскольку противолежащие стороны равны, то АNBQ параллелограмм. Задача В параллелограмме ABCD диагональ BD = 6 см и образует со сторонами AD и DC углы по 60 градусов. Определите углы и периметр параллелограмма ABCD. Дополнительно: определите вид четырехугольника ABMD, где точка M - середина DC, определите углы четырехугольника ABMD. 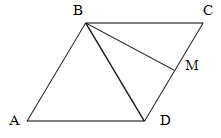Решение. Поскольку нам дана величина угла ADB (диагональ параллелограмма образует со сторонами AD и DC углы по 60 градусов), то величина угла DBC также равна 60 градусов, поскольку противоположные стороны параллелограмма параллельны, соответственно диагональ является секущей для двух параллельных прямых AD и BC, а для любой секущей внутренние накрест лежащие углы равны. Таким образом, в треугольнике BCD нам известны два угла из трех, и они оба равны 60 градусов. Соответственно, поскольку сумма углов треугольника равна 180 градусов, то угол BCD также равен 60 градусам, из чего следует, что треугольник BCD - равносторонний. Поскольку треугольник BCD - равносторонний, то BC = CD = BD = 6 см. Таким образом, поскольку противолежащие стороны параллелограмма равны, периметр его равен 24 см. Параллелограмм является ромбом. Дополнительно: Поскольку точка М лежит на стороне CD, то AB и MD - параллельны, следовательно, ABMD - трапеция. Угол DAB трапеции равен 60 градусов, исходя из решения, изложенного выше, как угол параллелограмма. Угол ADM равен 120 градусов, так как по условию диагональ BD образует со сторонами AD и DC углы по 60 градусов, а ADM равен сумме данных углов. Поскольку по условию точка M - середина DC, CM = MD. Значит BM - медиана треугольника DBC. Как указано выше, треугольник DBC - равносторонний, а в равностороннем треугольнике медиана является, одновременно, биссектрисой и высотой. Значит, угол DBM равен половине угла DBC и равен 60 / 2 = 30 градусов. Откуда угол ABM = 60 + 30 = 90 градусов. Поскольку BM - высота, то BMD равен также 90 градусов. Исходя из сказанного,  ABMD - прямоугольная трапеция. Ответ: 24 см. 60º, 90º, 90º, 120º - прямоугольная трапеция. 0    Параллелограмм. Задачи про площадь и стороны | Описание курса | Площадь параллелограмма

Записаться на курсы
Обратиться к консультанту
Пройти тест
Полный список курсов обучения
Нужна информация (помогите решить)