|
|
Примечание. Это часть урока с задачами по геометрии (раздел равнобедренный треугольник). Здесь размещены задачи, которые вызывают трудности при решении. Если Вам необходимо решить задачу по геометрии, которой здесь нет - пишите об этом в форуме. Для обозначения действия извлечения квадратного корня в решениях задач используется символ √ или sqrt(), при чем в скобках указано подкоренное выражение.
См. также описание и теоретические материалы на тему свойства и формула площади равнобедренного треугольника.
Задача.
Вершинами треугольника являются точки A(-2;1), B(-1;5), C(-6;2). Докажите, что треугольник ABC - равнобедренный.
Решение.
У равнобедренного треугольника две стороны равны. Чтобы доказать, что треугольник является равнобедренным, необходимо вычислить длину всех его сторон.
Применив формулу вычисления длины отрезка через координаты его точек, получим:
AB = sqrt( ( -2 - ( -1 ) )2 + ( 1 - 5 )2 ) = √( 1 + 16 ) = √17
BC = sqrt( ( -1 - ( -6 ) )2 + ( 5 - 2 )2 ) = √( 25 + 9 ) = √36 = 6
AC = sqrt( ( -2 - ( -6 ) )2 + ( 1 - 2 )2 ) = √( 16 + 1 ) =
√17
Как видно из расчетов, AB = AC равно корню квадратному из 17. Таким образом, треугольник ABC является равнобедренным
Задача.
Высота, проведённая к основанию равнобедренного треугольника равна 9 см, а само основание равно 24см. Найдите радиусы вписанной в треугольник и описанной около треугольника окружностей.
Решение.
Для решения задачи воспользуемся следующими формулами:
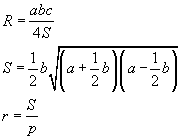
где:
R - радиус описанной окружности
r - радиус вписанной окружности
p - полупериметр треугольника
S - площадь треугольника, при чем формула нахождения площади треугольника приведена для равнобедренного треугольника и является следствием формулы Герона для случая, когда a - длины одинаковых сторон, а b - длина третьей стороны.
Сначала найдем длину одинаковых сторон равнобедренного треугольника. Поскольку высота, опущенная на основание равнобедренного треугольника, является одновременно и медианой, то, применив теорему Пифагора, получим:
a = √ (92 + 122 ) = √225 = 15
Теперь найдем площадь равнобедренного треугольника
S = 1/2 * 24 √ ( ( 15 + 1/2 * 24 ) ( 15 - 1/2 * 24 ) ) = 12 √ ( 27 * 3 ) = 12 √ 81 = 108 см2
Откуда радиус описанной окружности вокруг равнобедренного треугольника
R = 15 * 15 * 24 / ( 4 * 108 ) = 12.5 см.
Радиус вписанной окружности
p = ( 15 + 15 + 24 ) / 2 = 27
r = 108 / 27 = 4
Ответ: 4 и 12,5 см.
Равнобедренный треугольник |
Описание курса
| Рівнобедрений трикутник
|

