Задача:

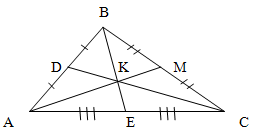
У трикутнику ABC медіани CD і BE перетинаються в точці К. Знайдіть площу чотирикутника ADKE, якщо BC = 20 см, AC = 12 см,
а кут ACB дорівнює 135 градусів.

Рішення:

1. Властивості медіан:
   • Медіани трикутника перетинаються в одній точці, яка називається центроїдом, і діляться цією точкою на дві частини у відношенні 2:1,
     рахуючи від вершини.
   • Трикутник ділиться трьома медіанами на шість рівновеликих трикутників.
2. Площа трикутника:
   • Площу трикутника можна знайти за формулою S=1/2 ab sin ⁡γ, де a і b - сторони трикутника, а γ - кут між ними.
   • Дано BC = 20 см, AC = 12 см, і ∠ACB=135°:

• Значення синуса 135 градусів: sin⁡135°=√2/2

1. Площа чотирикутника ADKE:
   • Чотирикутник ADKE утворений двома з шести рівновеликих трикутників.
   • Отже, його площа становить 1/3 від загальної площі трикутника:

Відповідь: Площа чотирикутника ADKE дорівнює 20√2 см².