Завдання

У правильній чотирикутній піраміді сторона основи дорівнює aa, висота дорівнює 3a3a. Знайдіть кути нахилу бічних ребер та
бічних граней до площини основи.

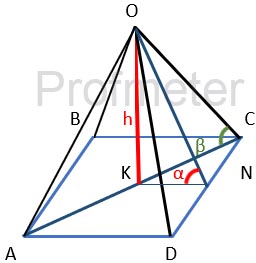
Розв'язання

Знайдемо кут нахилу ребер до площини основи.
Оскільки в основі правильної піраміди лежить правильний чотирикутник, то в даному випадку це квадрат.
Оскільки висота піраміди проектується у центр основи, це - точка перетину діагоналей.

Звідки KN = а/2

Трикутник OKN – прямокутний, OK – висота, рівна 3а.

Знайдемо тангенс кута KNO, позначивши його як α.

tg α = OK / KN
tg α = 3a / (a/2) = 6
α = arctg 6 ≈ 80.5377°

Знайдемо кут нахилу ребра піраміди.
Правильна чотирикутна піраміда має квадратну основу, тому діагональ основи можна
знайти за формулою:

d = AC = a√2

Діагоналі в точці перетину діляться навпіл.
Таким чином, для прямокутного трикутника OKC тангенс кута KCO (позначимо його як β ) дорівнює

tg β = OK / KC
tg β = 3a / (а√2/2) = 6 / √2
β = arctg 6/√2 ≈ 76.7373°

Відповідь: кут нахилу граней arctg 6 ≈ 80.5377 °; кут нахилу ребер arctg 6/√2 ≈ 76.7373°