Примітка. В цьому розділі формулювання і доведення теореми синусів. В уроках глави наведені завдання з геометрії з рішеннями на цю ж тему.
Див. також Теорема косинусів.   

Теорема синусів

Теорема синусів встановлює залежність між величиною кутів трикутника і протилежних йому сторін.

Формулювання теореми синусів

Сторони трикутника пропорційні синусам протилежних кутів

або,



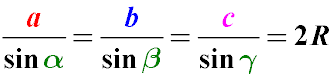
де
R - радіус описаного навколо трикутника кола
a, b, c - сторони трикутника
α, β, γ - величини протилежних цим сторонам кутів

Доказ теореми синусів

 
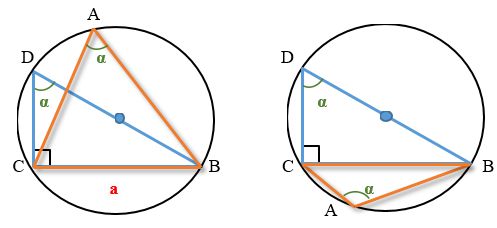
Доказ теореми синусів відбувається за допомогою додаткових побудов.

Побудуємо довільний трикутник, вписаний в коло. Позначимо його як ABC.
Додатково побудуємо діаметр окружності, в яку вписаний довільний трикутник, але так, щоб він проходив через один з його кутів. Діаметр дорівнює подвійному радіусу кола (2R).

Візьмемо до уваги, що однією з властивостей прямокутного трикутника, вписаного в коло є те, що його гіпотенуза, є діаметром кола, в яке він вписаний.

Позначимо діаметр для описаного кола як BD. Утворений трикутник BCD є прямокутним, оскільки його гіпотенуза лежить на діаметрі описаного кола (властивість кутів, вписаних в коло).

Таким чином, додатково побудований трикутник, у якого одна загальна сторона з побудованим раніше довільним трикутником, а гіпотенуза збігається з діаметром окружності - є прямокутним. Тобто трикутник DBC - прямокутний.
  
Для доказу всієї теореми, оскільки розміри трикутника ABC обрані довільним чином, досить довести, що співвідношення однієї довільної сторони до протилежного їй кута одно 2R. 

Нехай це буде 2R = a / sin α, тобто якщо взяти за кресленням 2R = BC / sin A. 

Оскільки, кути, вписані в коло, що спираються на одну й ту ж дугу, рівні, то кут CDB або дорівнює куту CAB (якщо точки A і D лежать по одну сторону від прямої BC), або дорівнює π - CAB (в іншому випадку).

Звернемося до властивостей тригонометричних функцій. Оскільки sin (π - α) = sin α, то зазначені варіанти побудови трикутника все одно призведуть до одного результату.

Обчислимо значення 2R = a / sin α, за кресленням 2R = BC / sin A. Для цього замінимо sin A на співвідношення відповідних сторін прямокутного трикутника.

2R = BC / sin A 
2R = BC / ( BC / DB ) 
2R = DB 

А, оскільки, DB будувався як діаметр кола, то рівність виконується.
Повторивши той же міркування для двох інших сторін трикутника, отримуємо: 



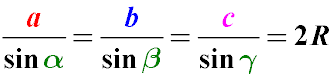
Теорема синусів доведена.