див. також синус деяких кутів (sin 60, sin 30, sin 45).

Синус кута

Для прямокутного трикутника ABC синусом (sin) кута A буде співвідношення сторін BC і AB.   

Синус кута прямокутного трикутника дорівнює відношенню катета, що протилежить, до гіпотенузи.   

sin A = BC / AB   

Значення функції синуса кута альфа в прямокутному трикутнику буде завжди однаковою для одного і того ж кута незалежно від розмірів сторін трикутника.

Функция синус угла (sin)

СИНУС (sin) - тригонометрична величина, функція кута, що змінюється зі зміною кута. «Синус» перекладається з латинської як «вигин», «кривизна».

 Рухаючи рухливий радіус по повному колу проти годинникової  стрілкi, одержимо позитивнi кути від 0° до 360°. 

Рухаючи рухливий радіус по повному колу за годинниковою стрілкою, виходять негативні кути, відповідно від 0° до -360°.

У прямокутному трикутнику сторона, що проти прямого кута, називається гіпотенузою, а інші сторони - катетами.

Синус гострого кута в прямокутному трикутнику є відношення протилежного катету до гіпотенузи.

 

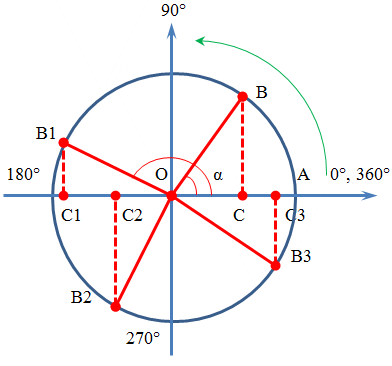
Розглянемо на окружності зміни функції синуса гострого кута, побудувавши на нерухомій стороні кута (ОА) катет прямокутного трикутника (ОС), у якого гіпотенузою буде рухливий радіус (ОВ). (Мал. 1).

За визначенням синуса кута: sin ⁡a=ВС / ОВ .

Для одиничної окружності, де ОВ = 1, це довжина відрізка ВС. Отже, синус кута - це величина проекції рухомого відрізка ОВ на вісь у.

Розглянемо зміни функції sin α (відрізка ВС) при русі рухомого радіуса окружності і збільшенні кута. Межі зміни синуса кута будемо визначати по квадрантах. 

У І квадранті ( ВС ):

при α = 0º sin α = 0;

при 0º < α < 90º 0 < sin α < 1;

при α = 90º sin α = 1.

У II квадранті ( В₁С₁ ):

при α = 90º sin α = 1;

при 90º < α < 180º 1 > sin α > 0;

при α = 180º sin α = 0.

За пройдений перше півколо sin α змінився від 0 до 0, а найбільше його значення, рівне 1, збігається з довжиною радіусу на позитивній півосі у.

Друге півколо руху рухомого радіуса можна розглядати як позитивний напрям (при русі ОВ далі проти годинникової стрілки) і як негативне спрямування (якщо ОВ обертати за годинниковою стрілкою). Розглянемо тільки позитивний напрямок.

В III квадранті ( В₂С₂ ):

при α = 180º sin α = 0;

при 180º < α < 270º 0 > sin α > -1;

при α = 270º sin α = -1;

В IV квадранті ( В₃С₃ ):

при α = 270º sin α = -1;

при 270º < α < 360º -1 < sin α < 0;

при α = 360º sin α = 0.

За пройдене друге півколо sin α змінився від 0 до 0, а найменше його значення, рівне -1, збігається з довжиною радіусу але від'ємній півосі. 
За весь оборот рухомого радіусу ОВ, від збігу з ОА до другого їх збігу, кут чисельно змінився від 0º до 360º, а чисельне значення синуса кута змінювалася в межах від 1 до-1.

див. також - таблиця значень основних кутів тригонометричних функцій.