Похідна логарифма

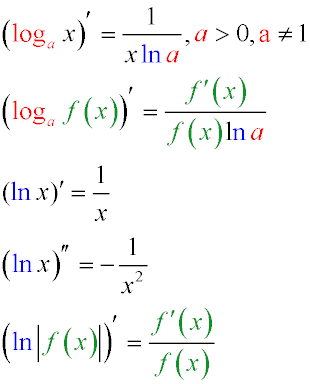
1. (loga x)' = 1/(x ln a)
   Похідна логарифма з основою а змінної ікс дорівнює одиниці, поділеної на твір змінної та натурального логарифму від а.
2. (loga f(x))' = f '(x) / (f(x) ln a)
   Похідна логарифма з основою а від функції f(x) дорівнює дробу, у чисельнику якого знаходиться похідна функції f(x),
   а в знаменнику - добуток f(x) та натурального логарифму від а
3. (ln x)' = 1/x 
   Похідна натурального логарифму дорівнює 1/х
4. (ln x)'' = - 1 / x²
   Подвійна похідна від натурального логарифму ікс дорівнює мінус одиниці, поділеній на квадрат ікс
5. (ln f(x) )' = f '(x) / f(x) 
   Похідна натурального логарифму від функції f(x) дорівнює дробу, в чисельнику якого знаходиться похідна цієї функції, 
   а в знаменнику – сама функція