|
См. также: более сложный уровень - сложение и вычитание дробей с алгебраическими выражениями и переменными.
Сложение и вычитание простых дробей
Для проведения операции вычисления сложения простых дробей руководствуются следующим алгоритмом:
Сложение и вычитание простых дробей с одинаковым знаменателем
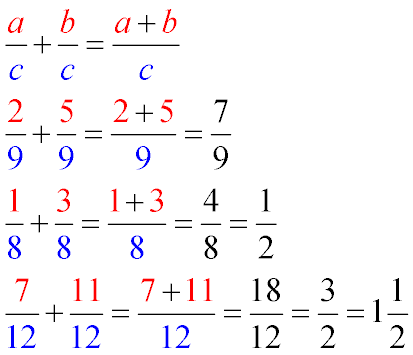 Для того, чтобы сложить две простые дроби с одинаковым знаменателем, необходимо сложить числители этих дробей, а знаменатель оставить без изменений.
- Числители каждой из дробей складываются, а знаменатели остаются без изменения
- При необходимости проводится сокращение дроби
- Если получившаяся дробь является неправильной (числитель больше знаменателя), дробь преобразуется в смешанную
Общая формула сложения простых дробей с одинаковым знаменателем приведена на картинке.
Примеры сложения дробей с одинаковыми знаменателями и их пояснение.
Складываем 2/9 и 5/9
Поскольку обе простые дроби имеют общий одинаковый знаменатель, то складываем числители
2+5 = 7
Ответ: 7/9
Складываем 1/8 и 3/8
Поскольку обе простые дроби имеют общий одинаковый знаменатель, то складываем числители
1+3=4
Таким образом, 1/8 + 3/8 = 4/8
Получившаяся дробь имеет кратные друг другу числитель и знаменатель, поэтому она подлежит сокращению. Сокращаем числитель и знаменатель на 4
4/8 = 1/2
Ответ: 1/2
Складываем 7/12 + 11/12
Поскольку обе простые дроби имеют общий одинаковый знаменатель, то складываем числители
7+11=18
Таким образом, 7/12 + 11/12 = 18/12
Получившаяся дробь имеет кратные друг другу числитель и знаменатель, поэтому она подлежит сокращению. Сокращаем числитель и знаменатель на 6
18/12 = 3/2
Получившаяся дробь является неправильной (числитель больше знаменателя). Преобразуем ее в смешанную
3/2 = 1 1/2
Ответ: 1 1/2
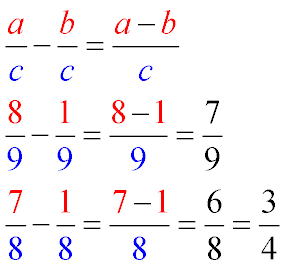 Для того, чтобы вычесть из одной простой дроби другую простую дробь, если обе дроби имеют одинаковый знаменатель, необходимо из числителя первой дроби, вычесть числитель второй дроби, а знаменатель оставить без изменения
- Из числителя первой дроби вычитается числитель второй дроби, а знаменатели остаются без изменения
- При необходимости проводится сокращение дроби
Примеры вычитания дробей с одинаковыми знаменателями и их пояснение.
Вычитаем: 8/9 - 1/9
Поскольку обе простые дроби имеют общий одинаковый знаменатель, то вычитаем из числителя первой дроби числитель второй дроби
8-1 = 7
Ответ: 8/9 - 1/9 = 7/9
Вычитаем: 7/8 - 1/8
Поскольку обе простые дроби имеют общий одинаковый знаменатель, то вычитаем из числителя первой дроби числитель второй дроби
7-1 = 6
Получившаяся дробь имеет кратные друг другу числитель и знаменатель, поэтому она подлежит сокращению. Сокращаем числитель и знаменатель на 2
6/8 = 3/4
Ответ: 7/8 - 1/8 = 3/4
В случае, когда обе дроби имеют разные знаменатели, пользуются правилами, описанными ниже.
Сложение и вычитание простых дробей с разными знаменателями (сложение и вычитание обыкновенных дробей)
Сложение обыкновенных дробей проводится по следующему алгоритму:
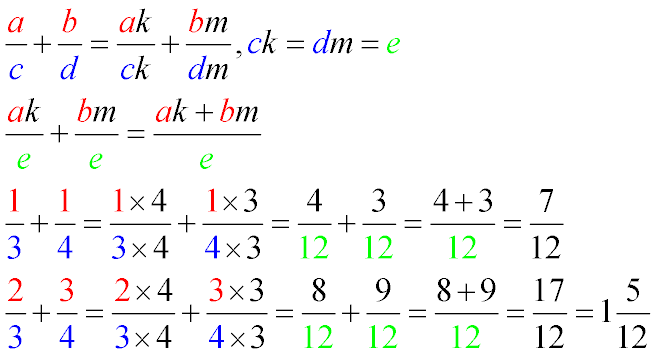
- Обе дроби приводятся к общему знаменателю
- Числители каждой из дробей складываются, а знаменатели остаются без изменения
- При необходимости проводится сокращение дроби
- Если получившаяся дробь является неправильной (числитель больше знаменателя), дробь преобразуется в смешанную
Примеры сложения простых дробей с разными знаменателями с пояснением.
Складываем 1/3 и 1/4
Поскольку знаменатели у обоих дробей - разные, их необходимо привести к общему знаменателю.
В данном случае, наименьшее общее кратное для 3 и 4 - это число 12. Соответственно, числитель и знаменатель первой дроби ( 1/3 ) умножаем на 4, а числитель и знаменатель второй дроби ( 1/4 ) умножаем на 3.
Получаем 4/12 и 3/12
Теперь у нас обе дроби имеют одинаковый знаменатель - 12. Поэтому складываем числители первой и второй дроби
4 + 3 = 7
Знаменатель остается без изменений 4/12 + 3/12 = 5/12
Ответ: 1/3 + 1/4 = 5/12
Складываем 2/3 и 3/4
Поскольку знаменатели у обоих дробей - разные, их необходимо привести к общему знаменателю.
В данном случае, наименьшее общее кратное для 3 и 4 - это число 12. Соответственно, числитель и знаменатель первой дроби ( 1/3 ) умножаем на 4, а числитель и знаменатель второй дроби ( 1/4 ) умножаем на 3.
Получаем 8/12 и 9/12
Теперь у нас обе дроби имеют одинаковый знаменатель - 12. Поэтому складываем числители первой и второй дроби
8 + 9 = 17
Знаменатель остается без изменений 8/12 + 9/12 = 17/12
Полученная дробь является неправильной (числитель больше знаменателя). Преобразуем ее в смешанную
17/12 = 1 5/12
Ответ: 2/3 + 3/4 = 1 5/12
Скорость поедания яблока |
Описание курса
| Сложение и вычитание дробей. Додавання і віднімання дробів
|

