|
|
Э́ллипс — геометрическое место точек X Евклидовой плоскости, для которых сумма расстояний от двух данных точек F1 и F2 (называемых фокусами)
постоянна, то есть | F1X | + | F2X | = 2a.
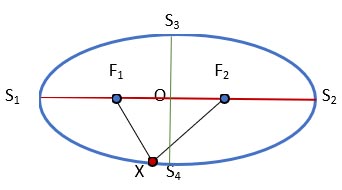
Общепринятые обозначения для формул, описывающих свойства эллипса указаны на рисунке:
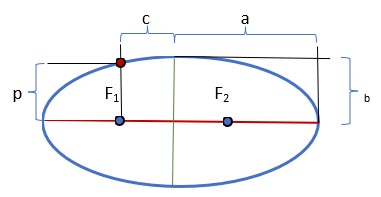
- Большая ось эллипса - это отрезок, проходящий через фокусы эллипса, ограниченный самим эллипсом.
Длина большой оси равна 2a.
- Малая ось эллипса - это отрезок, перпендикулярный большой оси эллипса, проходящий через ее центр, и ограниченный самим эллипсом.
Длина малой оси равна 2b.
- Большая и малая полуоси эллипса (a и b) - это отрезки, проведённые из центра эллипса к вершинам на большой и малой осях.
- Фокальное расстояние (c) - это расстояние от центра эллипса до его фокуса.
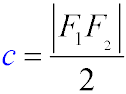
- Эксцентриситет (e) - это соотношение фокального расстояния и большой полуоси эллипса. Он однозначно характеризует величину "деформации"
эллипса по отношению к окружности и находится в интервале [0, 1). Ближе к нулю - ближе к окружности.
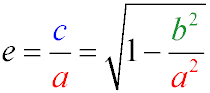
- Коэффициент сжатия эллипса - это отношение длин малой и большой полуосей. Если говорят про сжатие эллипса, то имеют ввиду значение (1-k)
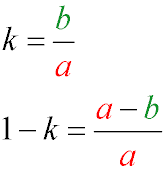
Для окружности коэффициент сжатия равен единице, сжатие — нулю.
- Коэффициент сжатия и эксцентриситет эллипса связаны соотношением
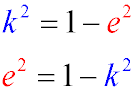
- Диаметром эллипса называется любая хорда, проходящая через его центр.
Пару диаметров, обладающих следующим свойством, называют сопряжёнными:
середины всех хорд, параллельных одному из них, расположены на втором диаметре.
Аналогично, середины хорд, параллельных второму диаметру, лежат на первом.
- Радиус эллипса в данной точке это отрезок, соединяющий центр эллипса с точкой, а также его длина, которая вычисляется по формуле
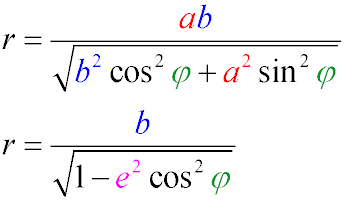
где φ — угол между радиусом и большой полуосью.
- Фокальный параметр — это половина длины хорды, которая проходит через фокус эллипса и перпендикулярна его большой оси
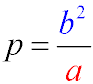
Каноническое уравнение эллипса
Для любого эллипса можно найти декартову систему координат такую, что эллипс будет описываться уравнением (каноническое уравнение эллипса):
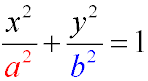
Каноническое уравнение эллипса описывает эллипс с центром в начале координат, оси которого совпадают с осями координат. Для определённости положим, что 0 < b ≤ a. В этом случае величины a и b — соответственно, большая и малая полуоси эллипса.
Зная полуоси эллипса можно вычислить его фокальное расстояние и эксцентриситет:
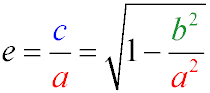
Координаты фокусов эллипса в этом случае будут (ae;0), и (-ae;0)
Эллипс имеет две директриссы, уравнения которых можно записать как
х = a / ε и х = - a / ε
Уравнение диаметра эллипса, сопряжённого хордам с угловым коэффициентом k:
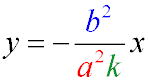
Уравнение касательных эллипса, проходящих через точку (x1y1)
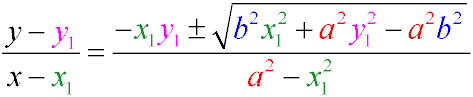
Уравнение касательных эллипса, имеющих данный угловой коэффициент k
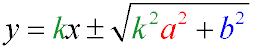
Уравнение нормали эллипса в точке (x1y1)
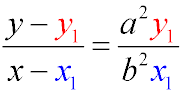
Примеры решения задач
Задача.
Найдите эксцентриситет эллипса
x2 / 8 + y2 / 6 = 1
Решение.
По формуле нахождения эксцентриситета эллипса (см. выше)
ε = √(64 - 36) / 8
ε = √28 / 8 = 2√7 / 8 = √7 / 4 ≈ 0,66 ≈ 2/3
Область определения функции |
Описание курса
| Свойства бесконечно малых и бесконечно больших функций
|

