Note. This is a lesson with solutions to geometry problems (cylinder section). If you need to solve a geometry problem that is not listed here,
please write about it in the forum. In the problems, the symbol "square root" may be replaced with the sign "√".
Problem
The axial section of a cylinder is a square with a diagonal of 4√2. Calculate the volume of the cylinder.
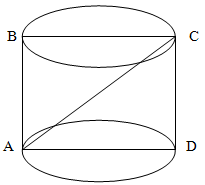
Solution
Since the diagonal of the section of the cylinder is a square, let us denote its side as aa.
a2+a2=(4√2)2
2a2=32
a2=16
a = 4
We find the volume of the cylinder using the formula:
V = πd2 / 4 ⋅ h
where
V=π 42 / 4 ⋅ 4
V = 16π
Answer: The volume of the cylinder is 16π
Problem
A cube with an edge length of aa is inscribed in a cylinder. Find the area of the axial section of the cylinder.
Solution
We draw a plane through the base of the cylinder.
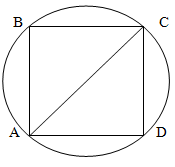
The diagonal of the cube is simultaneously the diameter of the cylinder. Knowing the side of the cube,
we determine the length of the diagonal AC of the square ABCD as:
CD2+AD2=AC2
a2+a2 = AC2
2a2=AC2
AC = a√2
We draw a plane through the axis of the cylinder along the diagonal ACAC. The height of the section is equal to the edge length of the cube and,
according to the problem conditions, is aa, and the width of the section is a√2.
Thus, the area of the section is:
S = a⋅a√2 = a2√2
Answer: a2√2
Problem
The diagonal of the axial section of a cylinder is 12 cm and forms an angle of 45 degrees with the plane of the lower base.
Find the volume of the cylinder.
Solution
Since the base of the axial section forms a right angle with the height of the cylinder, the triangle formed by the diagonal of the axial section,
the height of the cylinder, and its diameter is a right triangle.
Based on this, the angle between the diagonal and the height is also 45 degrees (180 - 90 - 45).
Thus, the triangle is isosceles, and therefore, the height of the cylinder is equal to its diameter. Applying the Pythagorean theorem, we find them:
d2 + d2 = 122
2d2 = 144
d2 = 72
Now we apply the formula for the volume of the cylinder:
V = пd2 / 4 h
V = 72п / 4 * √72
V = 18п * √72 = 18 * 6 √2
Answer: 108π√2
Problem
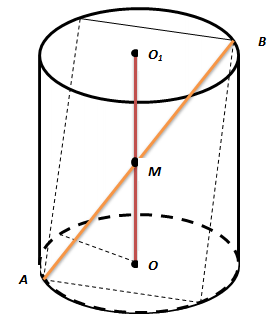
The height of the cylinder is 2 m. The radius of the base is 7 m.
A square is inscribed obliquely in this cylinder so that all its vertices lie on the circles of the bases.
Find the side of the square.
Solution
Due to the symmetry of the square and the cylinder and the fact that the square is oblique, the diagonal of the square intersects the axis
of the cylinder OO1 at point M, which is the midpoint of the segment OO1. According to the conditions, OO1= 2 m, and OA=7 m,
so OM = 1 m. Let d be the diagonal of the square.
Then the side of the square aa is equal to:
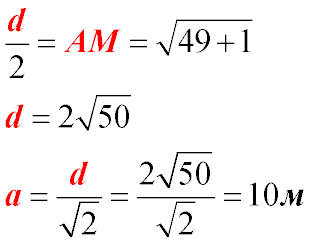
Cylinder with inscribed prism problems |
Описание курса
| Axial section of the cylinder
|

