Right prism
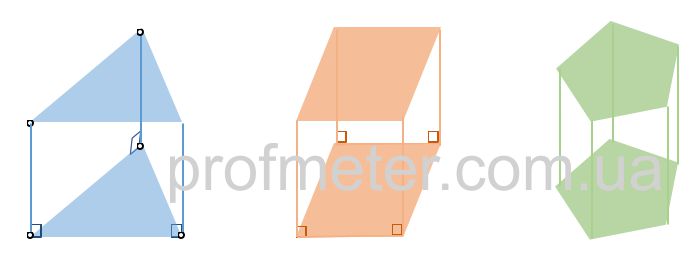
A right prism is a type of prism in which the lateral edges are perpendicular to the base. This means that the sides
of the prism stand upright, forming right angles with the base.
A right prism can have any geometric shape as its base, whether it be a triangle, square, pentagon, or any other polygon.
A regular right prism is a special type of right prism where the bases are regular polygons. This means that all sides
and angles of the base are equal.
For example, a regular right quadrangular prism is a type of parallelepiped. A parallelepiped is a three-dimensional
figure whose faces are parallelograms. A special case of a parallelepiped is a cube, which is a regular prism where
all faces are equal squares.
Properties of a Right Prism
- Equal Bases: The bases of a right prism are congruent, meaning they are identical in shape and size.
- Rectangular Lateral Faces: Each of the lateral faces of a right prism is a rectangle.
- Parallel and Equal Lateral Edges: The lateral edges are parallel to each other and are of equal length.
- Equal Rectangular Lateral Faces in Regular Prisms: In a regular right prism, the lateral faces are equal rectangles.
- Diagonal Plane Intersection: When a right prism is intersected by a diagonal plane, the resulting section is a parallelogram.
- Perpendicular Section: A section that is perpendicular to the lateral edges of the prism is also perpendicular to all lateral faces.
- Linear Angles of Dihedral Angles: The angles of the perpendicular section are the linear angles of the dihedral angles at the corresponding lateral edges.
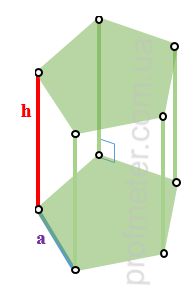
- Height and Edge Length: The length of the lateral edge of a right prism is equal to its height.
These properties make right prisms a fundamental concept in geometry, with applications in various fields such as architecture, engineering, and mathematics.
Right prism formulas
Where:
Ss - lateral surface area of a right prism
Sb - base area
V - volume of a right prism
Vn - volume of a right prism with a regular polygon at the base
Ssn - lateral surface area of a right prism with a regular polygon at the base
P - base perimeter
h - height of the prism, also known as the length of the lateral edge of a right prism
n - for a right prism with a regular polygon at the base, the number of sides of the regular polygon
a - for a right prism with a regular polygon at the base - the length of the side of the regular polygon
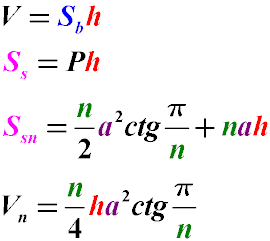
Rectangular Prism |
Описание курса
| Regular quadrangular prism
|

