|
Note. The text of the task is taken from the forum. If you did not find a solution to your task, write about it on the forum.
Task: Probability of Simultaneous Arrival of Steamships
Two ships must approach the same berth. The arrival time of both ships is independent and equally possible during
the day. Determine the probability that one of them will have to wait for the berth to be vacated if the parking time
of the first ship is six hours and the second is eight hours.
Solution
To determine the probability that one of the ships will have to wait for the berth to be vacated, consider the following:
-
Parking time of the first ship (T1): 6 hours
-
Parking time of the second ship (T2): 8 hours
-
Total time of the day (T): 24 hours
The arrival time of both ships is independent and equally possible during the day. This means that each ship can
arrive at any time during 24 hours with equal probability.
To solve the problem, we will use a geometric approach. Let's imagine a plane with axes X and Y, where X is the
time of the first ship's arrival, and Y is the time of the second ship's arrival. Both axes have a length of 24 hours.
On this plane, we can construct a square of size 24x24, where each point (x, y) represents the time of the arrival
of both ships.
Now consider the conditions under which one of the ships will have to wait for the berth to be released. This will
happen if the parking time of one ship overlaps with the parking time of the other ship. That is, if:
Let's combine these conditions into one: |x - y| < 6 or |x - y| < 8.
On the plane, this means that we have two strips of width 6 hours and 8 hours, which are located along the diagonal
of the square. The total width of the strips, where one of the steamships will have to wait, is 6 + 8 = 14 hours.
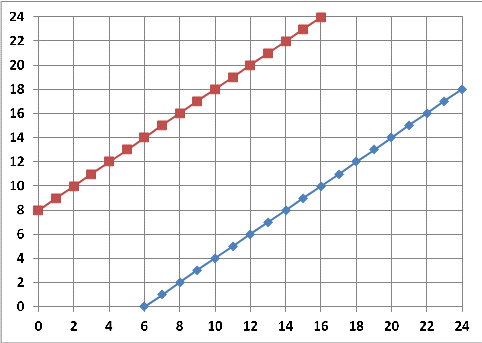
Probability of Arrival of Steamships
As we can see, the arrival time of one steamship is indicated on the x-axis, and the other on the y-axis. Thus, both
steamships will not "interfere" with each other if their arrival time (x, y) is lower than the blue line or higher than
the red one.
The common locus of the steamship arrival options, as can be seen from the graphs, is located on the plane of
the "square" with a side of 24 hours. Thus, the ratio of the area between the two lines to the total area of the square
will reflect the probability that one of the steamships will have to wait for the berth to be released while the other is parked.
The desired area can be found by calculating the definite integral of functions on the interval [0;24], but for simplicity
of solution, we will choose a more visual method.
- Find the area of the triangle bounded by the blue line:
S1=(24−6)×(24−6)2=162
- Find the area of the triangle bounded by the red line:
S2=(24−8)×(24−8)2=128
- Calculate the total area of the square:
Total Area=24×24=576
- Calculate the area that geometrically reflects the probability of the event:
Desired Area=576−128−162=286
- Calculate the probability of waiting for the vacating of the berth:
Probability=286/576=143/288≈0.49653
Answer: approximately 49.65%.
Probability theory |
Описание курса
|

